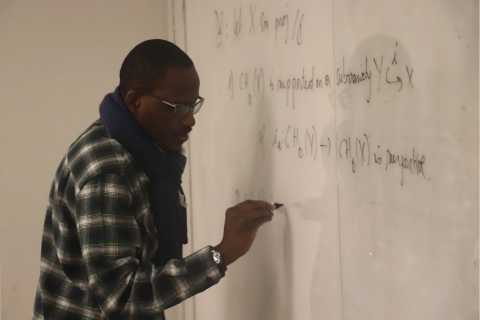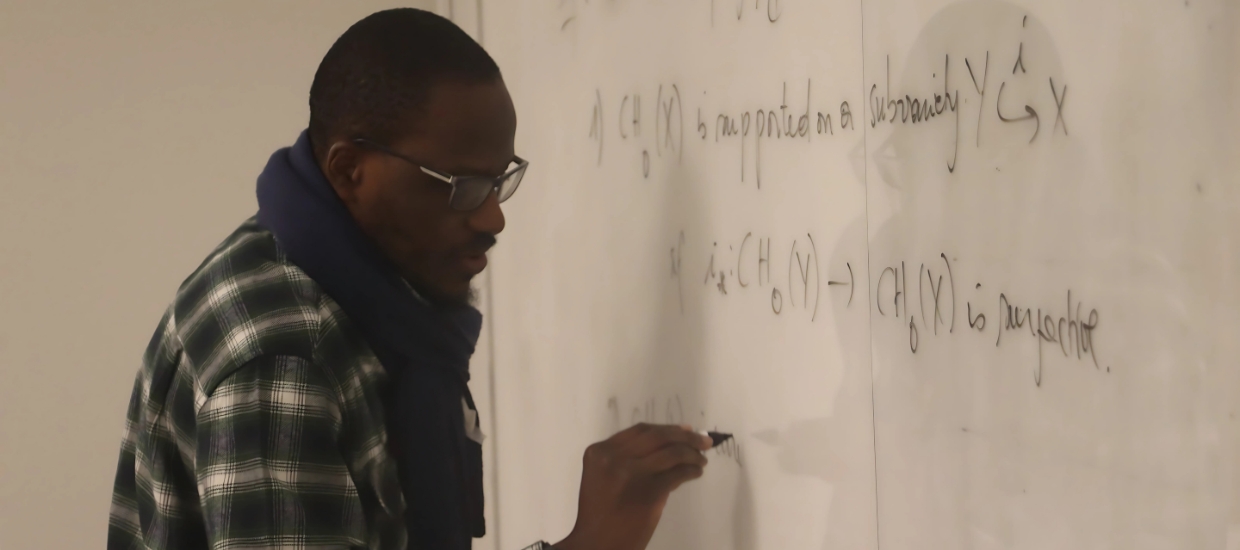Dates: January 23 & 24, 2025
Location: Ungar Bldg, Room 528B, 1365 Memorial Dr, Coral Gables, FL 33146
Live Video Available via Zoom
To register, click here
Schedule
Thursday, January 23, 2025
| 2:00pm |
Paolo Cascini, Imperial College London: On the birational geometry of algebraically integrable foliations
I will report regarding some recent results on the Minimal Model Program for algebraically integrable foliations and some of their applications. Video
|
| 3:00pm |
Ivan Cheltsov, University of Edinburgh: Which cubic 3-folds are rational?
By the beautiful theorem of Clemens and Griffiths, all smooth cubic 3-folds are irrational. On the other hand, all singular complex cubic 3-folds (except cones over smooth cubic curves) are known to be rational. In this talk, we will survey what is known about rationality of singular real cubic 3-folds - some of them are rational and some of them are irrational. This is a joint work with Yuri Tschinkel and Zhijia Zhang from New York. Video
|
| 4:00pm |
Phillip Griffiths, IAS & UM: “Invariants of normal functions” (Talk based on correspondence and ongoing work with Mark Green and Rodolfo Aguilar.)
Normal functions originally arose in the works of Picard and Poincaré in algebraic geometry as a method for studying curves C on an algebraic surface S using the intersections of C with the curves in a generic pencil of hypersurface sections of S. This method was then used by Lefschetz as a central ingredient in his proof of the famous (1,1) theorem. Normal functions have since been generalized and provide a Hodge-theoretic method for studying both the local and global properties of algebraic cycles varying in a family of generically smooth algebraic varieties. In recent years there have been significant developments in the theory. These include the understanding of the singularities of normal functions, the use of normal functions in physics (as multi-valued sections of Lagrangian fibrations, the study of D-branes,..), and the introduction and use of higher normal functions in arithmetic questions (study of regulators, ..). In fact these two strands may be intertwining, as been noted in the physics literature but has yet to materialize. There are two basic essentially algebraic invariants associated to the transcendental normal functions. One of these is the infinitesimal invariant delta(v), and the other is the inhomogeneous Picard-Fuchs equation Pv=f. An interesting question is how is: How related is the information in theses two invariants? There are some general structural results that set a context, but the richness of the theory resides in the specific examples. In this talk we will explain some of this story, focusing on the case of Calabi-Yau (CY) 3-folds. Similar results seem to be present for the case of CY pairs (X,Y) where X is Fano and Y is an anti-canonical divisor. Video
|
| 5:00pm |
Ludmil Katzarkov, UM: The theory of Atoms
We will introduce new birational invariants. Examples and relation with othe birational invariants will be considered. More examples will be considered in the talk of L. Cavenaghi. Video
|
| 6:00pm |
Reception
|
Friday, January 24, 2025
| 1:00pm |
Arman Sarikyan, The Maxwell Institute: Linearisation problem for the plane Cremona group
One of the main challenges in equivariant birational geometry is the classification of finite subgroups of the group of birational automorphisms of the n-dimensional projective space, also known as the Cremona group. To address this problem, it is natural to first classify subgroups of the Cremona group that are conjugate to subgroups acting biregularly on the n-dimensional projective space, i.e., subgroups of PGL(n+1). Such subgroups are called linearisable. While the Cremona group coincides with PGL(2) for n=1, it turns out that already for n>1, the classification becomes more intricate. In this talk, we will present a complete classification of the linearisable subgroups of the Cremona group for n=2. Video
|
| 2:00pm |
Leonardo Cavenaghi, CAMPINAS: Atoms meet symbols
In this talk, we add the needed concepts to the "Theory of Atoms" recently introduced by Katzarkov-Kontsevich-Pantev-Yu and show how one can combine it with the "symbols" introduced by Tschinkel-Kontsevich in 2019 in the frame of $G$-equivariant birational geometry, to obtain a new $\mathbb Z$-module that retains $G$-equivariant birational geometric information. We derive certain $\mathbb Z$-values $G$-equivariant birational invariants from that.
This is a joint work with L. Grama, L. Katzarkov, and M. Kontsevich. Video
|
| 3:00pm |
Zhijia Zhang, New York University: The volume preserving Cremona group
In this talk, we study the group of birational automorphisms of projective spaces that preserve the standard torus-invariant volume forms with logarithmic poles. This group is of interest in birational geometry due to its close connection to the theory of log Calabi-Yau pairs. In particular, we show that this group is not generated by pseudo-regularizable maps, and it is not simple. This extends a recent result on the Cremona group by Lin and Shinder. This is joint work with Konstantin Loginov. Video
|
| 4:00pm |
Rene Mboro, UM: Remarks on varieties of essential ${\rm CH}_0$-dimension at most 2.
We present the notion (due to Voisin) of essential ${\rm CH}_0$-dimension of a variety a give sufficient conditions for a variety with trivial group of 0-cycles and essential ${\rm CH}_0$-dimension at most 2 to have, in fact, essential ${\rm CH}_0$-dimension 0 (i.e. to admit a Chow-theoretic decomposition of the diagonal). Video
|
| 5:00pm |
Kaiqi Yang, UM: Potentially stably rational conic bundle over non-closed field
In this talk, we will explore the cohomological (H1) obstruction to the stable rationality of conic bundles over non-closed fields. This obstruction imposes specific conditions on the generators of the associated Galois group. The cohomological condition is preserved under orbit decomposition. Furthermore, we demonstrate the existence of several distinct classes of groups that satisfy the (H1) condition. Video
|
| 6:00PM |
Kyoung-Seog Lee, POSTECH: Motivic aspects of generalized logarithmic transformations
Logarithmic transformation is an important operation introduced by Kodaira in 1960s. One can obtain an elliptic surface with multiple fibers by performing logarithmic transformations on an elliptic surface without multiple fibers. Logarithmic transformation is a wild analytic operation and therefore it is hard to follow how algebro-geometric information changes under logarithmic transformation in general. In this talk, I will discuss motivic aspects of generalized logarithmic transformations via o-minimal geometry. This talk is based on a joint work with Ludmil Katzarkov, Ernesto Lupercio and Laurent Meersseman. Video
|